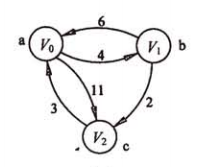
如果我们要求每一顶点对之间的最短路径，怎么做呢？

方法1：对N个顶点，依次执行前面的Prim算法。

方法2：使用Floyd算法。

实际上，Floyd算法是动态规划(DP)算法。

原理很简单，我们假设dp[i][j]表示从顶点i到顶点j的最短路径，则dp[i][j] = min (dp[i][k]+dp[k][j], 0<=k<=nvexs)。

于是算法如下：

import java.util.LinkedList;

public class Floyd {

	public void SetGraph(Graph g) {
		this.g = g;
	}

	public void ShortPath() {
		// Alloc dp array and load all arc data
		int pre[][] = new int[g.vexs.length][];
		int dp[][] = new int[g.vexs.length][];
		for (int i = 0; i < g.vexs.length; i++) {
			dp[i] = new int[g.vexs.length];
			pre[i] = new int[g.vexs.length];
			for (int j = 0; j < g.vexs.length; j++) {
				dp[i][j] = g.matrix[i][j];
				pre[i][j] = g.matrix[i][j];
				if (dp[i][j] != Integer.MAX_VALUE) {
					pre[i][j] = i;
				} else {
					pre[i][j] = -1;
				}
			}
		}
		// DP
		for (int i = 0; i < g.vexs.length; i++) {
			for (int j = 0; j < g.vexs.length; j++) {
				// dp[i][j] = min(dp[i][k]+dp[k][j])
				for (int k = 0; k < g.vexs.length; k++) {
					if (dp[i][k] != Integer.MAX_VALUE
							&& dp[k][j] != Integer.MAX_VALUE) {
						if (dp[i][k] + dp[k][j] < dp[i][j]) {
							dp[i][j] = dp[i][k] + dp[k][j];
							pre[i][j] = pre[k][j];
						}
					}
				}
			}
		}
		// Print
		LinkedList<Integer> stk = new LinkedList<Integer>();
		for (int i = 0; i < g.vexs.length; i++) {
			for (int j = 0; j < g.vexs.length; j++) {
				if (i != j) {
					System.out.format("%d -> %d short_path is %d\n", g.vexs[i],
							g.vexs[j], dp[i][j]);
					// Stack push
					stk.push(j);
					int tmp = j;
					while (tmp != i) {
						tmp = pre[i][tmp];
						stk.push(tmp);
					}
					// Output
					if (!stk.isEmpty()) {
						System.out.format("%d", stk.pop());
					}
					while (!stk.isEmpty()) {
						System.out.format("->%d", stk.pop());
					}
					System.out.println();
				}
			}
		}
	}

	private Graph g = null;

	public static void main(String[] args) {
		Graph g = new Graph();
		g.input();
		Floyd fld = new Floyd();
		fld.SetGraph(g);
		fld.ShortPath();
	}
}

关于图的读取和创建，我们借用之前Prim算法的Graph类，如下：

import java.util.Arrays;
import java.util.Scanner;

public class Graph {

	public Graph() {
		scan = new Scanner(System.in);
	}

	public void input() {
		intput_vexs();
		input_arcs();
	}

	private void intput_vexs() {
		// Input vexs
		int nvexs = 0;
		System.out.println("Please enter n for vexs:");
		if (scan.hasNextInt()) {
			nvexs = scan.nextInt();
		}
		vexs = new int[nvexs];
		for (int i = 0; i < nvexs; i++) {
			System.out.println("Please enter a integer for vex(" + i + "):");
			if (scan.hasNextInt()) {
				vexs[i] = scan.nextInt();
			}
		}
	}

	private void input_arcs() {
		// Input weight between vexs
		int nvexs = vexs.length;
		matrix = new int[nvexs][];
		for (int i = 0; i < nvexs; i++) {
			matrix[i] = new int[nvexs];
			Arrays.fill(matrix[i], Integer.MAX_VALUE);
		}
		int narcs = 0;
		int x = 0, y = 0, w = 0;
		System.out.println("Please enter n for arcs:");
		if (scan.hasNextInt()) {
			narcs = scan.nextInt();
		}
		for (int i = 0; i < narcs; i++) {
			System.out.println("Please enter x, y, w for arc(" + i + "):");
			if (scan.hasNextInt()) {
				x = scan.nextInt();
				x = vex2i(x);
			}
			if (scan.hasNextInt()) {
				y = scan.nextInt();
				y = vex2i(y);
			}
			if (scan.hasNextInt()) {
				w = scan.nextInt();
			}
			if (x == -1 || y == -1 || w <= 0) {
				System.out.println("x or y or w invalid, please enter again:");
				i--;
			} else {
				matrix[x][y] = w;
			}
		}
	}

	public int vex2i(int v) {
		for (int i = 0; i < vexs.length; i++) {
			if (v == vexs[i]) {
				return i;
			}
		}
		return -1;
	}

	public int[][] matrix = null;
	public int[] vexs = null;
	private Scanner scan = null;

	public static void main(String[] args) {
		Graph g = new Graph();
		g.input();
		System.out.println("vexs:");
		for (int i = 0; i < g.vexs.length; i++) {
			System.out.print(g.vexs[i] + " ");
		}
		System.out.println();
		System.out.println("matrix:");
		for (int i = 0; i < g.matrix.length; i++) {
			for (int j = 0; j < g.matrix[i].length; j++) {
				System.out.format("%11d ", g.matrix[i][j]);
			}
			System.out.println();
		}
	}
}

测试图：

测试输入：

3
0
1
2
5
0 1 4
1 0 6
0 2 11
2 0 3
1 2 2

输出：

0 -> 1 short_path is 4
0->1
0 -> 2 short_path is 6
0->1->2
1 -> 0 short_path is 5
1->2->0
1 -> 2 short_path is 2
1->2
2 -> 0 short_path is 3
2->0
2 -> 1 short_path is 7
2->0->1