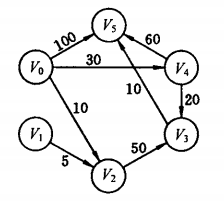
单源最短路径：给定带权有向图和源点v，求从v到G中其余各点的最短路径。

Dijkstra算法非常类似于最小生成树算法(的Prim)。

算法：

0、假设源为v0，设置辅助变量dist和pre，优先队列pq，按照dist[x]从小到达排序（小顶堆）。

1、如果v0->i连通，初始化dist[i]为w[v0][i]。放(dist[i], i)入pq。

2、循环，直到pq为空。

2.1、取出pq中最小的，设其下标为x，

2.2、遍历图matrix[x][i], i 0->nvexs。如果dist[x]+matrix[x][i] < dist[i]，更新dist[i]=dist[x]+matrix[x][i]，并且放(dist[i], i)入pq，并且pre[i] = x。

3、如果dist[i]<INFINTE，输出dist[i]，并倒序输出pre[?]直到为-1。

上述这么搞，时间复杂度应该为O(nlogn)

好了，代码如下：

图及输入

import java.util.Arrays;
import java.util.Scanner;

public class Graph {

	public Graph() {
		scan = new Scanner(System.in);
	}

	public void input() {
		intput_vexs();
		input_arcs();
	}

	private void intput_vexs() {
		// Input vexs
		int nvexs = 0;
		System.out.println("Please enter n for vexs:");
		if (scan.hasNextInt()) {
			nvexs = scan.nextInt();
		}
		vexs = new int[nvexs];
		for (int i = 0; i < nvexs; i++) {
			System.out.println("Please enter a integer for vex(" + i + "):");
			if (scan.hasNextInt()) {
				vexs[i] = scan.nextInt();
			}
		}
	}

	private void input_arcs() {
		// Input weight between vexs
		int nvexs = vexs.length;
		matrix = new int[nvexs][];
		for (int i = 0; i < nvexs; i++) {
			matrix[i] = new int[nvexs];
			Arrays.fill(matrix[i], Integer.MAX_VALUE);
		}
		int narcs = 0;
		int x = 0, y = 0, w = 0;
		System.out.println("Please enter n for arcs:");
		if (scan.hasNextInt()) {
			narcs = scan.nextInt();
		}
		for (int i = 0; i < narcs; i++) {
			System.out.println("Please enter x, y, w for arc(" + i + "):");
			if (scan.hasNextInt()) {
				x = scan.nextInt();
				x = vex2i(x);
			}
			if (scan.hasNextInt()) {
				y = scan.nextInt();
				y = vex2i(y);
			}
			if (scan.hasNextInt()) {
				w = scan.nextInt();
			}
			if (x == -1 || y == -1 || w <= 0) {
				System.out.println("x or y or w invalid, please enter again:");
				i--;
			} else {
				matrix[x][y] = w;
			}
		}
	}

	public int vex2i(int v) {
		for (int i = 0; i < vexs.length; i++) {
			if (v == vexs[i]) {
				return i;
			}
		}
		return -1;
	}

	public int[][] matrix = null;
	public int[] vexs = null;
	private Scanner scan = null;

	public static void main(String[] args) {
		Graph g = new Graph();
		g.input();
		System.out.println("vexs:");
		for (int i = 0; i < g.vexs.length; i++) {
			System.out.print(g.vexs[i] + " ");
		}
		System.out.println();
		System.out.println("matrix:");
		for (int i = 0; i < g.matrix.length; i++) {
			for (int j = 0; j < g.matrix[i].length; j++) {
				System.out.format("%11d ", g.matrix[i][j]);
			}
			System.out.println();
		}
	}
}

Dijkstra算法：

import java.util.Comparator;
import java.util.PriorityQueue;

class DijPair {

	public DijPair(int i, int w) {
		this.i = i;
		this.w = w;
	}

	public int i;
	public int w;
}

public class Dijkstra {

	public void SetGraph(Graph g) {
		this.g = g;
	}

	public void ShortPath(int start) {
		// Convert start to position
		int v = g.vex2i(start);
		if (v == -1) {
			System.out.println("start vex " + start + " invalid");
		}
		// PriorityQueue
		PriorityQueue<DijPair> pq = new PriorityQueue<DijPair>(10,
				new Comparator<DijPair>() {
					@Override
					public int compare(DijPair a, DijPair b) {
						return a.w - b.w;
					}
				});
		// Init dist & pre
		int dist[] = new int[g.vexs.length];
		int pre[] = new int[g.vexs.length];
		for (int i = 0; i < g.matrix[v].length; i++) {
			pre[i] = -1;
			dist[i] = g.matrix[v][i];
			if (dist[i] != Integer.MAX_VALUE) {
				pre[i] = v;
				pq.add(new DijPair(i, dist[i]));
			}
		}
		// While not empty
		while (!pq.isEmpty()) {
			// Pool the smallest w and it's i
			DijPair cur = pq.poll();
			if (cur == null) {
				break;
			}
			// Update dist if smaller
			for (int i = 0; i < g.matrix[cur.i].length; i++) {
				if (g.matrix[cur.i][i] != Integer.MAX_VALUE
						&& dist[cur.i] + g.matrix[cur.i][i] < dist[i]) {
					dist[i] = dist[cur.i] + g.matrix[cur.i][i];
					pre[i] = cur.i;
					pq.add(new DijPair(i, dist[i]));
				}
			}
		}
		// End
		for (int i = 0; i < dist.length; i++) {
			if (dist[i] != Integer.MAX_VALUE) {
				System.out.format("short_dist %d to %d is %d ", start,
						g.vexs[i], dist[i]);
				System.out.print(", path is ");
				System.out.format("%d ", g.vexs[i]);
				int tmp = pre[i];
				while (tmp != -1) {
					System.out.format("<- %d ", g.vexs[tmp]);
					tmp = pre[tmp];
				}
				System.out.println();
			}
		}
	}

	private Graph g = null;;

	public static void main(String[] args) {
		Graph g = new Graph();
		g.input();
		Dijkstra dij = new Dijkstra();
		dij.SetGraph(g);
		dij.ShortPath(0);
	}
}

测试图：

测试数据：

6
0
1
2
3
4
5
8
0 5 100
0 2 10
0 4 30
1 2 5
2 3 50
4 3 20
3 5 10
4 5 60

测试输出：

short_dist 0 to 2 is 10 , path is 2 <- 0
short_dist 0 to 3 is 50 , path is 3 <- 4 <- 0
short_dist 0 to 4 is 30 , path is 4 <- 0
short_dist 0 to 5 is 60 , path is 5 <- 3 <- 4 <- 0