假设要在n个城市之间建立通信网络，则连通n个城市只需要n-1条线路。现在想节省光缆，使得路径和最小。

这一问题就是最小代价生成树问题(Minimum Cost Spanning Tree)，简称MST。

MST性质：假设N=(V, {E})是一个连通图，U是顶点集合V的一个非空子集，若(u, v)是一条具有最小权值的边，u属于U且v属于V-U。则必存在一棵包含边(u, v)的最小生成树。

因此，可以采用贪心算法解决。

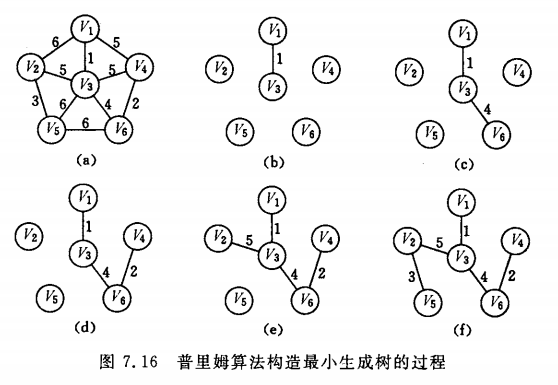
1、Prim(普里姆)算法

我们需要设置两个辅助数组cost和ivex，它们需要联合在一起使用。

i表示一个尚未被选择的顶点的下标(尚属于V-U)。cost[i]为U中所有顶点中到i的最小权值，ivex[i]即为U中的这个顶点。

因此初始情况下，我们使得ivex[*] = v0, cost[i] = arcs[v0][i]。

每次，选择cost最小的一个的i，然后ivex[i]就是新选择边的起始点，i就是终结点。

代码如下：

#include <stdio.h>
#include <stdlib.h>
#include <memory.h>

#define MAX_VNUM 100
#define INF_DIST 0xfffffff
#define COST_SELECT -1

typedef struct
{
	int vexs[MAX_VNUM]; // vertex(s)
	int nvexs; // number of vertex(s)
	int arcs[MAX_VNUM][MAX_VNUM]; // arc(s)
	int narcs; // number of arc(s)
} Graph;

int graph_locate_vec(Graph* graph, int val)
{
	int i;
	for(i=0; i<graph->nvexs; i++)
	{
		if(graph->vexs[i]==val)
		{
			return i;
		}
	}
	return -1;
}

void graph_create_graph(Graph* graph)
{
	int i, j;
	// 存储顶点
	printf("Please enter n for vex(s) :\n");
	scanf("%d", &graph->nvexs);
	for(i=0; i<graph->nvexs; i++)
	{
		printf("Please enter a int for vecs(%d) :\n", i);
		scanf("%d", &graph->vexs[i]);
	}
	// 存储弧度
	//memset(graph->arcs, INF_DIST, sizeof(int)*MAX_VNUM*MAX_VNUM);
	for(i=0;i<graph->nvexs;i++)
	{
		for(j=0;j<graph->nvexs;j++)
		{
			graph->arcs[i][j] = INF_DIST;
		}
	}
	printf("Please enter m for arc(s) :\n");
	scanf("%d", &graph->narcs);
	for(i=0; i<graph->narcs; i++)
	{
		int x, y, w;
		printf("Please enter v1, v2, w for vecs(%d) :\n", i);
		scanf("%d %d %d", &x, &y, &w);
		x = graph_locate_vec(graph, x);
		y = graph_locate_vec(graph, y);
		if(x==-1 || y==-1)
		{
			i--;
			printf("Invalid v1 or v2.\n");
			continue;
		} else if (w<=0)
		{
			i--;
			printf("Invalid w.\n");
			continue;
		}
		graph->arcs[x][y] = w;
		graph->arcs[y][x] = w;
	}
}

// Minimum Cost Spanning Tree using Prim
void mst_prim(Graph* g)
{
	int k;
	int i;
	int j;
	int ivex[MAX_VNUM];
	int cost[MAX_VNUM];
	k = 0; // First vec in U
	cost[k] = COST_SELECT;
	// Init cost with u -> i (i is vex in V-U)
	for(i=0; i<g->nvexs; i++)
	{
		if(i!=k)
		{
			ivex[i] = k;
			cost[i] = g->arcs[k][i];
		}
	}
	// Select other nvex-1
	for(i=1; i<g->nvexs; i++)
	{
		// Select min cost[i] and i is not select yet
		int min=INF_DIST, min_vex=0;
		for(j=0; j<g->nvexs; j++)
		{
			if(cost[j]!=COST_SELECT && cost[j]<min)
			{
				min_vex = j;
				min = cost[j];
			}
		}
		k = min_vex;
		cost[k] = COST_SELECT;
		printf("Arc %d -> %d \n", g->vexs[ivex[k]], g->vexs[k]);
		// Update unselect cost
		for(j=0; j<g->nvexs; j++)
		{
			if(cost[j]!=COST_SELECT && g->arcs[k][j]<INF_DIST && g->arcs[k][j]<cost[j])
			{
				ivex[j] = k;
				cost[j] = g->arcs[k][j];
			}
		}
	}
}

int main()
{
	Graph g;
	graph_create_graph(&g);
	mst_prim(&g);
	return 0;
}

测试图如下：

测试数据：

6
1
2
3
4
5
6
10
1 2 6
1 3 1
1 4 5
2 3 5
2 5 3
3 4 5
3 5 6
3 6 4
4 6 2
5 6 6

上面实线的这个Prim算法的时间复杂读是O(n^2)，主要耗费在选取min cost上。而这一过程，可以用堆(优先队列)实现，使得复杂度降低为O((V+E)*logV)。

由此，Prim算法适用于稠密图中求最小生成树。

2、Kruskal(克鲁斯卡尔)算法

Kruskal适用于稀疏图中求最小生成树。

时间复杂度是O(E log E) 或者 O(E log V)

Kruskal算法的流程非常简单明了，但需要借助两个数据结构：

(1) 堆(优先队列)，按照每条Arc的weight，每次取出最小的weight的Arc。
(2) 并查集，用于判断两个顶点vex i和vex j是否属于同一个结合，并可做合并操作。

算法流程：

• create a forest F (a set of trees), where each vertex in the graph is a separate tree
• create a set S containing all the edges in the graph
• while S is nonemptyand F is not yet spanning
  • remove an edge with minimum weight from S
  • if that edge connects two different trees, then add it to the forest, combining two trees into a single tree
  • otherwise discard that edge.

由于实在不喜欢STL的优先队列，用Java实现吧。

首先是并查集，一定不要实现错哦！

public class UFSet {

	public UFSet(int n) {
		parent = new int[n];
		for (int i = 0; i < n; i++) {
			parent[i] = i;
		}
	}

	public int Find(int i) {
		// check
		if (i < 0 || i >= parent.length) {
			return -1;
		}
		// Find until root and remember it
		if (parent[i] != i) {
			parent[i] = Find(parent[i]);
		}
		return parent[i];
	}

	public void Union(int i, int j) {
		if (i < 0 || j < 0 || i >= parent.length || j >= parent.length) {
			return;
		} else {
			int pi = Find(i);
			int pj = Find(j);
			parent[pi] = pj;
		}
	}

	private int parent[] = null;

	public static void main(String[] args) {
		int n = 10;
		UFSet set = new UFSet(n);
		set.Union(0, 3);
		set.Union(0, 4);
		for (int i = 0; i < n; i++) {
			System.out.println(set.Find(i));
		}
	}
}

然后是Kruskal算法，input是输入参数，kruskal是算法正常执行。

import java.util.Scanner;
import java.util.Comparator;
import java.util.PriorityQueue;

public class Kruskal {

	class Arc {

		public int getX() {
			return x;
		}

		public void setX(int x) {
			this.x = x;
		}

		public int getY() {
			return y;
		}

		public void setY(int y) {
			this.y = y;
		}

		public int getWeight() {
			return weight;
		}

		public void setWeight(int weight) {
			this.weight = weight;
		}

		public Arc(int a, int b, int w) {
			x = a;
			y = b;
			weight = w;
		}

		private int x; // ivex for start
		private int y; // ivex for end
		private int weight;
	};

	int vex2i(int vexs[], int v) {
		for (int i = 0; i < vexs.length; i++) {
			if (v == vexs[i]) {
				return i;
			}
		}
		return -1;
	}

	public void input() {

		// Scanner
		Scanner scan = new Scanner(System.in);

		// Get vexs
		int nvexs = 0;
		System.out.println("Please enter the number of vexs:");
		if (scan.hasNextInt()) {
			nvexs = scan.nextInt();
		}
		vexs = new int[nvexs];
		for (int i = 0; i < nvexs; i++) {
			System.out.println("Please enter a integer for vex[" + i + "]:");
			if (scan.hasNextInt()) {
				vexs[i] = scan.nextInt();
			}
		}

		// PriorityQueue to store arcs
		pq = new PriorityQueue<Arc>(100, new Comparator<Arc>() {
			@Override
			public int compare(Arc a1, Arc a2) {
				return a1.getWeight() - a2.getWeight();
			}
		});

		// Get arcs
		int narcs = 0;
		System.out.println("Please enter the number of arcs:");
		if (scan.hasNextInt()) {
			narcs = scan.nextInt();
		}
		for (int i = 0; i < narcs; i++) {
			System.out.println("Please enter x y w for arc[" + i + "]:");
			int x = -1, y = -1, w = 0;
			if (scan.hasNextInt()) {
				x = scan.nextInt();
				x = vex2i(vexs, x);
			}
			if (scan.hasNextInt()) {
				y = scan.nextInt();
				y = vex2i(vexs, y);
			}
			if (scan.hasNextInt()) {
				w = scan.nextInt();
			}
			if (x == -1 || y == -1) {
				System.out.println("x or y invalid.");
				i--;
				continue;
			}
			if (w <= 0) {
				System.out.println("w invalid.");
				i--;
				continue;
			}
			Arc arc = new Arc(x, y, w);
			pq.add(arc);
		}
	}

	public void kruskal() {
		// Union-Find Set
		UFSet ufset = new UFSet(vexs.length);
		// while not pq.empty, select min arc.w
		double ans = 0.0;
		while (!pq.isEmpty()) {
			Arc arc = pq.poll();
			int x = arc.getX();
			int y = arc.getY();
			int px = ufset.Find(x);
			int py = ufset.Find(y);
			if (px == py) {
				continue;
			} else {
				System.out.println("Arc " + vexs[x] + " ->" + vexs[y] + "");
				ufset.Union(x, y);
				ans += arc.getWeight();
			}
		}
		System.out.println("Final mst: " + ans);
	}

	private int vexs[] = null;
	private PriorityQueue<Arc> pq = null;

	public static void main(String[] args) {
		Kruskal kruskal = new Kruskal();
		// Input vexs and arcs
		kruskal.input();
		// Doing Kruskal
		kruskal.kruskal();
	}

}

输出结果：

Arc 1 ->3
Arc 4 ->6
Arc 2 ->5
Arc 3 ->6
Arc 2 ->3
Final mst: 15.0