对于一个连通图,如果删除了结点v以及相关联的边之后,图被分割成了两个或以上的连通分量,则称v是该图的一个关节点(articulation point),也叫割点。
如果一个图中不存在关节点(割点),则该图为重连通图(biconnected graph)。显然重连通图是很稳定的,例如一个航空网络是重连通的,则当某调航线因为外部条件被破坏,那么旅客总可以从别的航线绕道到达目的地。
如果在连通图上至少要删除k个顶点才能破坏图的连通性,则称此图的连通度为k。
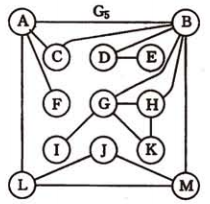
对于如下的连通图G:
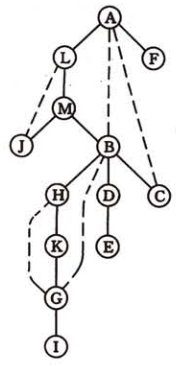
我们进行DFS遍历,得到如下的一棵深度优先遍历树:
实线是邻接点组成的父亲、孩子关系。虚线是回边连接的祖先、结点关系。
1、对任意顶点v,它的双亲结点和会变连接的祖先结点是它之前搜索到的邻接点。
2、对于任意顶点v,它的孩子结点是在v之后搜索到的邻接点。
为此,我们可以用visit[v]表示访问到v时是第几个号(如果从访问的第一个结点开始算1的话)。若访问到v时,它的邻接点w已经访问过,则w是v的双亲结点或回边连接的(DFS优先树的)祖先结点。如果w未曾访问过,则w是v的(DFS优先树)孩子结点。
我们还可以得到如下两个结论:
1、若生成树的根有两棵或以上的子树,则此顶点必为割点。
2、若生成树中某个非叶子结点v,其某棵子树的根和子树中其他结点均没有指向v的祖先的回边,则v为关节点。
为此我们可以再定义一个数组low[v] = Min(low[w], visit[v], visit[k]),其中w是v的(DFS树的)孩子结点,k是v的(DFS树的)回边连接的祖先结点。
由此,若low[w] >= visit[v],v必为割点。
我们可以用改造的DFS算法求出图中的所有割点。
int count = 1;
void graph_dfs_inner(struct Graph* g, int* visit, int* low, int v)
{
struct Arc* ptr = g->vexs[v].first_arc;
int min = visit[v] = ++count;
while(ptr!=NULL)
{
if(!visit[ptr->ivex])
{
// ptr is v's child
graph_dfs_inner(g, visit, low, ptr->ivex);
if(low[ptr->ivex]<min)
{
min = low[ptr->ivex];
}
if(low[ptr->ivex]>=visit[v])
{
printf("Gedian: %d\n", g->vexs[v].data);
}
} else
{
// ptr is v's ans
if(visit[ptr->ivex]<min)
{
min = visit[ptr->ivex];
}
}
ptr = ptr->next;
}
low[v] = min;
}
void graph_dfs(struct Graph* g)
{
struct Arc* ptr = NULL;
int i;
int visit[MAX_VEXS];
int low[MAX_VEXS];
memset(visit, 0, sizeof(int)*MAX_VEXS);
memset(low, 0, sizeof(int)*MAX_VEXS);
visit[0] = count = 1;
ptr = g->vexs[0].first_arc;
graph_dfs_inner(g, visit, low, ptr->ivex);
if(count < g->nvexs)
{
// Root has at least two sub-tree, is gedian
printf("Gedian: %d\n", g->vexs[0].data);
while(ptr!=NULL)
{
if(!visit[ptr->ivex])
{
graph_dfs_inner(g, visit, low, ptr->ivex);
}
ptr = ptr->next;
}
}
}
测试数据,以本文前面的连通图为例:
13 1 2 3 4 5 6 7 8 9 10 11 12 13 17 1 2 1 3 1 6 1 12 2 3 2 4 2 7 2 8 2 13 4 5 7 9 7 11 7 8 8 11 10 12 10 13 12 13
割点:
Gedian: 4 Gedian: 2 Gedian: 7 Gedian: 2 Gedian: 1