1、在图结构中，结点关系是任意的：任意两个数据元素(结点)之间都可能有关系。

2、有向图可以表示为G={V, A}，V是顶点集合，A是关系(边)的集合，也可称作VR。关系(边)用有序对<v, w>表示。图形表示是一条有向弧。v是初始点(弧尾)，w是终端点(狐头)。

3、无向图一般表示为G={V, E}，V还是顶点集合，E是边集合。边用无序对(v, w)表示。图形表示是一条边(无向)。

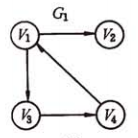
有向图G1：

V1 = {v1, v2, v3, v4}

A1 = {<v1, v2>, <v1, v3>, <v3, v4>, <v4, v1>}

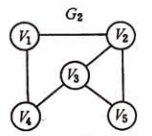
无向图G2：

V2 = {v1, v2, v3, v4}

E2 = {(v1, v4), (v1, v2), (v2, v3), (v2, v5), (v3, v4), (v3, v5)}

4、完全图：具有n(n-1)/2条边的无向图，n为顶点数目。

5、有向完全图：具有n(n-1)条边的有向图，n为顶点数目。

6、稀疏图：e<nlogn，e为边数，n为顶点数目。反之为稠密图。

7、网：图的边或弧上有相关的数叫做权。

8、子图：假设两个图G=(V, {E})和G'=(V', {E'})，如果V'属于V并且E’属于E，则称G‘为G的子图。

9、邻接点：对于无向图G={V, {E}}，如果边(v, v')属于E，则v和v'互为邻接点。

入度、出度的概念只对有向图而言！

10、入度：对于某个顶点，弧指向的边为入度。

11、出度：对于某个顶点，弧发出的边为出度。

例如对于下述图G1的顶点v1，入度是1，出度是2。

12、对于有向图，入度、出度与边的关系是：

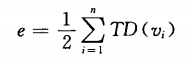13、路径：对于无向图G=(V, {E})，v到v'的路径路径是指顶点序列(v=v12, v....vxv')，其中所有顶点都是V中的顶点。

14、回路(环)：路径的第一个顶点和最后一个顶点相同。

15、简单路径：路径的顶点序列中，任意顶点都不重复出现。

16、连通：如果顶点v到v'之间有路径。

17、连通图：图中任意两个顶点vi和vj，都是连通的，则G是连通图。

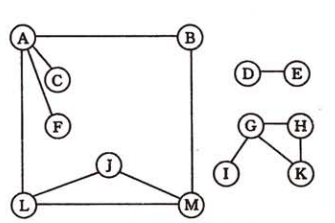
18、连通分量：指无向图中的极大连通子图。 比如下面的非连通图中，有3个连通分量。

18、强连通图：对于图G中任意一对点vi和vj，从vi到vj和从vj到vi都存在路径，则G是强连通图。

19、强连通图未必是完全图！

20、强连通分量：极大强联通子图称作有向图的强连通分量。

21、生成树：是连通图的极小连通子图，含有图中全部顶点，但只有足以构成连通的n-1条边(n是结点数量)。

22、如果一个图中有n个顶点和小于n-1条边，那么他一定是非连通图。

23、生成树一定有n-1条边，但有n-1条边的不一定就是生成树。

这节概念真多。。。