树的存储，不再限于二叉树了。

1、双亲标示法
虽然每个结点可能有多个孩子，但是每个孩子只可能有一个双亲，这是固定的。
于是有了双亲标示法。
每个孩子存在数组中，孩子记录其双亲的位置。
如果根据某个孩子找双亲，可以几乎在常数时间搞定(反复调用PARENT(T, X)，直到X为根为止)。
但是如果要从树根往下遍历求孩子结点，则需要遍历整个数组，会很慢。

typedef struct PTNode
{
int data;
int parent;
};

typdef struct
{
PTNode nodes[MAX_TREE_SIZE];
int r, n; //根的位置，实际结点总数。
}PTree;

2、孩子表示法
由于每个结点可能有多颗子树，所以可以用多重链表，即每个结点有多个指针域，其中每个指针指向医科子树的根结点。
定义如下：
typedef struct CTNode
{
int data; // data
struct CTNode* children; // link list, ended with NULL
}*CTree;

3、孩子兄弟标示法
又叫二叉树/二叉链表标示法。即把树存储转化为二叉链表表示。
两个链表分别是第一个孩子结点和下一个兄弟结点。
typedef struct CSNode
{
int data;
struct CSNode* firstchild, *nextsibling;
}CSNode, *CSTree;

这种表示方法非常方便，例如要访问x结点的第i个孩子，只需要x->firstchild，然后沿着nextsilbing指针走i-1次即可。

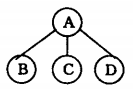
例如，我们有如下的树：

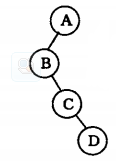
转化为二叉链表后表示是这样的：

森林与二叉树的转换

这种转换拓展了上述“树的二叉链表表示法”

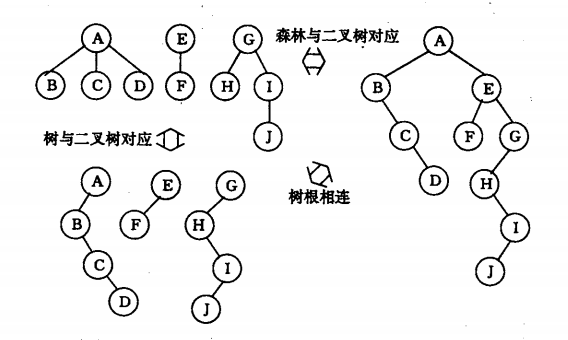
首先，我们第一树的根R作为整个森林二叉树的根。

然后，将二叉链表表示法拓展一下，将第一棵的孩子作为在R的左子树。而其他树作为"nextSilmbing"，依次接在R的右子树上。

最终效果如下图：

 树的遍历

对于树(单棵，但可能不止两个子树)，有先根遍历和后根遍历两种方式。(注意显然没有中根遍历，因为不止左、右两个子树了)。

例如下面的子树：

 

先根遍历：A B C D E

后根遍历：B D C E A

森林的遍历

对于森林遍历，有先序和中序遍历两种情况。

先序遍历森林：

先访问第一棵树的根结点；
先序遍历第一课树的根结点的子树森林；
先序遍历除去第一棵树之后剩余的树构成的森林；

例如上面A~J的树，先序遍历森林的结果就是：A  B  C  D  E  F  G  H  I  J

实际就是对应的二叉链表表示的二叉树的先序遍历。

中序遍历森林：

中序遍历森林中第一棵子树的根结点的子树森林；
访问第一棵树的根结点；
中序遍历除去第一棵树之后剩余树构成的森林；

例如上面A~J的树，中序遍历森林的结果是：B  C  D  A  F  E  H  J  I  G

实际就是对应的二叉链表表示的二叉树的中序遍历。