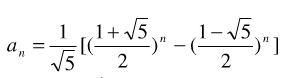堆栈与递归是相辅相成的。

比如Fibnacci数列就是递归定义：

Fib(n) = Fib(n-1) + Fib(n-2) (n>=2) Fib(0) = 0 Fib(1) = 1

Fibnacci数列：1, 1, 2, 3, 5, 8, 13, 21, ....

说到这里再写个Fibnacci的通项公公式：

这个还是很无敌的……

然后再一个例子是书上的Ackerman函数：

转回经典的汉诺塔问题：假设有三个命名为X，Y，Z的塔座，在X上插有n个执行大小各不相同、从小到达的圆盘1~n。现在要求将X上的n个圆盘移动到塔座Z上，并能依然按从小到达排列，每次只能移动一个，任何时候不能将大的放在小的上面。

思路：

当n=1时，直接把标号为1的从X诺到Z就可以了。

当n>1时，首先要把n之上的n-1个圆盘从塔座X移到塔座Y上（借助Z）。然后将n从X移动到Z上。然后再将n-1个圆盘移动到Z上，此时就是一个递归过程了。

代码如下：

#include <stdio.h>

int move(int n, char src, char dst)
{
    printf("move %d from %c to %c \n", n, src, dst);
}

// Move disk #n from x to z with help of y
void hanoi(int n, int x, int y, int z)
{
    if(n==1)
    {
        move(1, x, z);
    }else
    {
        hanoi(n-1, x, z, y);
        move(n, x, z);
        hanoi(n-1, y, x, z);
    }
}

int main()
{
    hanoi(3, 'x', 'y', 'z');
    return 0;
}

下面是一个4层汉诺塔的移动方法：

move 1 from x to y
move 2 from x to z
move 1 from y to z
move 3 from x to y
move 1 from z to x
move 2 from z to y
move 1 from x to y
move 4 from x to z
move 1 from y to z
move 2 from y to x
move 1 from z to x
move 3 from y to z
move 1 from x to y
move 2 from x to z
move 1 from y to z

递归的一些其他事情：

1、先调用先返回的原则

2、调用函数和被调用函数之间的链接和信息交换要通过栈来进行。

3、没进入一层递归，就产生一个新的工作记录压入栈顶。每退出一层递归，就从栈顶弹出一个工作记录。当前正在执行的叫做活动记录。