本文是转载的，《B树、B-树、B+树、B*树》
B树
即二叉搜索树：
1.所有非叶子结点至多拥有两个儿子（Left和Right）；
2.所有结点存储一个关键字；
3.非叶子结点的左指针指向小于其关键字的子树，右指针指向大于其关键字的子树；
如：
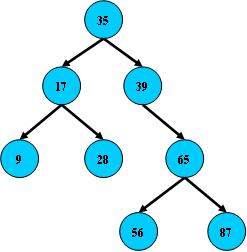B树的搜索，从根结点开始，如果查询的关键字与结点的关键字相等，那么就命中；
否则，如果查询关键字比结点关键字小，就进入左儿子；如果比结点关键字大，就进入右儿子；如果左儿子或右儿子的指针为空，则报告找不到相应的关键字[......]
大二那会根本没蹋下心来看，觉得天书一般，连旋转都没搞明白。
今天仔细看了书，发现真的一点不难啊，鄙视自己……
首先是概念：
平衡二叉树是为了解决前面二叉排序树不均衡的问题，而加入了一种平衡机制。所以，平衡二叉树是一种特殊的二叉排序树(BST)！
AVL树查找的平均和最差复杂度都是O(logn) ！！！(BST的最坏是O(n))
AVL树的插入复杂度是O(logn)。
平衡二叉树（简称AVL树）：对任意一个结点，它的左子树和又子树都是平衡二叉树（左子树都小于结点[......]
1、前面讨论了静态查找表，它们的特点是，数据是一次性就给好了。
2、而对于动态查找表，数据可以是在查找过程中动态添加、生成的。其实这概念不太严谨。
3、二叉排序树(BST)：左子树上所有结点的值均小于根结点的值；右子树上所有结点的值均大于根结点上的值。
4、二叉排序树的查找过程：
(1)若树为空，直接返回/跳出。
(2)树非空，则
(a)若key==root.data，return true。
(b)若key<root.data, root = root.left[......]
概念明天补上。。。
顺序查找，用了哨兵，减少检查数组长度的次数，据说这样可以让顺序查找的性能提升一倍。
优点：无序任何假设条件（如数组有序等）。
缺点：效率低。
#include <stdio.h>
int ssearch(int* arr, int n, int key)
{
int i = 0;
arr[n] = key;
for(i=0;arr[i]!=key;i++);
if(i==n)
{[......]
如果我们要求每一顶点对之间的最短路径，怎么做呢？
方法1：对N个顶点，依次执行前面的Prim算法。
方法2：使用Floyd算法。
实际上，Floyd算法是动态规划(DP)算法。
原理很简单，我们假设dp[i][j]表示从顶点i到顶点j的最短路径，则dp[i][j] = min (dp[i][k]+dp[k][j], 0<=k<=nvexs)。
于是算法如下：
import java.util.LinkedList;
public class Fl[......]